Dual LED Flasher

 
 

          The circuit above is actually a multivibrator, i.e. a free-running miltivibrator. It's identical to a flip-flop that triggers itself repeatedly. Q1 and Q2 are general purpose PNP transistors (2N3906, 2N2907, etc). R1 and R2 limit the current to the LEDs (which flash alternately). Increasing the values of C1 and C2 will slow the flash rate.


   

HJSplit (Software for Splitting and Joining File)

    

HJ-Split is a software that can be used to split and join a file with very easy steps.

How to split files:
1. run HJ-Split and select Split
2. select the file you want to split (input file)
3. specify the location of the split (output file)
4. You can specify the partition size of the file you want on the split file size option (in KB or MB)
5. click start
6. DONE!

How to join files (only for files that are splitted using HJ-Split):
1. run HJ-Split and select Join
2. select the file you want to join (input file), ie files with extension .001
3. specify the location of the join
4. click start
5. DONE!

Download HJ-Split

Have fun.. ;-)

[update] ISIS Proteus Simulator 7.6 SP4

    
    

Here's I give you the newer version of ISIS Proteus Simulator, a powerful tool for learning about electronics circuit (the previous version of Proteus Simulator that I share on this blog is version 7.1). Here's the screenshot:

 

It looks much better and it has an attractive UI, and of course supported also by libraries that are richer than ever. You can see it in the component mode and then pick the device, seen many new components that do not exist in version 7.1. Hope You like it. Have fun :-)


For direct and easily download, this file is partitioned into several sections. You can merge the files of this partition using HJSplit software.

Download Proteus Simulator 7.6 SP4 (total file size is 68 MB)
part1
part2
part3
part4

Note: for Windows Vista and Windows 7 you must run it as an administrator by right click on the file and select "run as an administrator".

if You have never known what it was Proteus Simulator, here's the introduction ;-)


What is Proteus Simulator?

555 Timer Chip

       
          The 555 timer chip is probably the most versatile non-programmable part I have ever seen. Over the past 40 years, many people have created at least hundreds probably thousands of applications that have used this chip in ways I’m sure the original designer never would have thought possible; the original function of the chip was to provide a regular train of pulses. In this section, I will show how the chip is used in a circuit, along with some of the tricks that can be performed with it.

The 555 is usually built into an eight pin ‘‘dual in-line package’’ that is commonly used for chips. In Figure above, I have put in an ‘‘overhead’’ view of the 555, along with a photograph of an actual 555 chip.
          Looking at the labels for each of the pins, most of them do not make a lot of sense. What should jump out at you is the ‘‘Gnd’’ (ground) at Pin 1 and the ‘‘Vcc’’ (positive power) at Pin 8. These two pins are used to provide power for the part; they match the power pins I’ve presented elsewhere for digital devices elsewhere in the book.
          To try and get a better understanding of a chip, I'll discussed with detail explanation about this topic later, wait for my next posting..


to be continued..


 

The Multivibrator

 
   
          Multivibrators, like the familiar sinusoidal oscillators, are circuits with regenerative feedback, with the difference that they produce pulsed output. There are three basic types of multivibrator, namely the Bistable Multivibrator, the Monostable Multivibrator and the Astable Multivibrator.

1. Bistable Multivibrator

          A bistable multivibrator circuit is one in which both LOW and HIGH output states are stable. Irrespective of the logic status of the output, LOW or HIGH, it stays in that state unless a change is induced by applying an appropriate trigger pulse. As we will see in the subsequent pages, the operation of a bistable multivibrator is identical to that of a flip-flop.

          Figure 1 shows the basic bistable multivibrator circuit. This is the fixed-bias type of bistable multivibrator. Other configurations are the self-bias type and the emitter-coupled type. However, the operational principle of all types is the same. The multivibrator circuit of Fig. 1 functions as follows. In the circuit arrangement of Fig. 1 it can be proved that both transistors Q₁ and Q₂ cannot be simultaneously ON or OFF. If Q₁ is ON, the regenerative feedback ensures that Q₂ is OFF, and when Q₁ is OFF, the feedback drives transistor Q₂ to the ON state. In order to vindicate this statement, let us assume that both Q₁ and Q₂ are conducting simultaneously. Owing to slight circuit imbalance, which is always there, the collector current in one transistor will always be greater than that in the other. Let us assume that I_C2 > I_C1. Lesser I_C1 means a higher V_C1. Since V_C1 is coupled to the Q₂ base, a rise in V_C1 leads to an increase in the Q₂ base voltage. Increase in the Q₂ base voltage results in an increase in I_C2 and an associated reduction in V_C2 Reduction in V_C2 leads to a reduction in Q₁ base voltage and an associated fall in I_C1, with the result that V_C1 increases further. Thus, a slight circuit imbalance has initiated a regenerative action that culminates in transistor Q₁ going to cut-off and transistor Q₂ getting driven to saturation. To sum up, whenever there is a tendency of one of the transistors to conduct more than the other, it will end up with that transistor going to saturation and driving the other transistor to cut-off. Now, if we take the output from the Q₁ collector, it will be LOW (= V_CE1 sat.) if Q₁ was initially in saturation. If we apply a negative-going trigger to the Q₁ base to cause a decrease in its collector current, a regenerative action would set in that would drive Q₂ to saturation and Q₁ to cut-off. As a result, the output goes to a HIGH (=+V_CC) state. The output will stay HIGH until we apply another appropriate trigger to initiate a transition. Thus, both of the output states, when the output is LOW and also when the output is HIGH, are stable and undergo a change only when a transition is induced by means of an appropriate trigger pulse. That is why it is called a bistable multivibrator.

2. Monostable Multivibrator

          A monostable multivibrator, also known as a monoshot, is one in which one of the states is stable and the other is quasi-stable. The circuit is initially in the stable state. It goes to the quasi-stable state when appropriately triggered. It stays in the quasi-stable state for a certain time period, after which it comes back to the stable state.

          Figure 2 shows the basic monostable multivibrator circuit. The circuit functions as follows. Initially, transistor Q₂ is in saturation as it gets its base bias from +V_CC through R. Coupling from Q₂ collector to Q₁ base ensures that Q₁ is in cut off. Now, if an appropriate trigger pulse induces a transition in Q₁ from saturation to cut-off, the output goes to the HIGH state. This HIGH output when coupled to the Q₁ base turns Q₁ ON. Since there is no direct coupling from Q₁ collector to Q₂ base, which is necessary for a regenerative process to set in, Q₁ is not necessarily in saturation. However, it conducts some current. The Q₁ collector voltage falls by I_C1R_C1 and the Q₂ base voltage falls by the same amount, as the voltage across a capacitor (C in this case) cannot change instantaneously. To sum up, the moment we applied the trigger, Q₂ went to cut off and Q₁ started conducting. But now there is a path for capacitor C to charge from V_CC through R and the conducting transistor. The polarity of voltage across C is such that the Q₂ base potential rises. The moment the Q₂ base voltage exceeds the cut-in voltage, it turns Q₂ ON, which, owing to coupling through R₁, turns Q₁ OFF. And we are back to the original state, the stable state. Whenever we trigger the circuit into the other state, it does not stay there permanently and returns back after a time period that depends upon R and C. The greater the time constant RC, the longer is the time for which it stays in the other state, called the quasi stable state.

3. Astable Multivibrator

          In the case of an astable multivibrator, neither of the two states is stable. Both output states are quasistable. The output switches from one state to the other and the circuit functions like a free running square-wave oscillator.

          Figure 3 shows the basic astable multivibrator circuit. It can be proved that, in this type of circuit, neither of the output states is stable. Both states, LOW as well as HIGH, are quasi-stable. The time periods for which the output remains LOW and HIGH depends upon R₂C₂ and R₁C₁ time constants respectively. For R₁C₁= R₂C₂, the output is a symmetrical square waveform. The circuit functions as follows. Let us assume that transistor Q₂ is initially conducting, that is, the output is LOW. Capacitor C₂ in this case charges through R₂ and the conducting transistor from V_CC, and, the moment the Q₁ base potential exceeds its cut in voltage, it is turned ON. A fall in Q₁ collector potential manifests itself at the Q₂ base as voltage across a capacitor cannot change instantaneously. The output goes to the HIGH state as Q₂ is driven to cut-off. However, C₁ has now started charging through R₁ and the conducting transistor Q₁ from VCC. The moment the Q2 base potential exceeds the cut-in voltage, it is again turned ON, with the result that the output goes to the LOW state. This process continues and, owing to both the couplings (Q₁ collector to Q₂ base and Q₂ collector to Q₁ base) being capacitive, neither of the states is stable. The circuit produces a square-wave output.

   

ISIS Proteus Simulator (Electronics Software)

 
 
  

Proteus is software for microprocessor simulation, schematic capture, and printed circuit board (PCB) design. It is developed by Labcenter Electronics.

Proteus Virtual System Modelling (VSM) combines mixed mode SPICE circuit simulation, animated components and microprocessor models to facilitate co-simulation of complete microcontroller based designs. For the first time ever, it is possible to develop and test such designs before a physical prototype is constructed.

This is possible because you can interact with the design using on screen indicators such as LED and LCD displays and actuators such as switches and buttons. The simulation takes place in real time (or near enough to it): a 1GMHz Pentium III can simulate a basic 8051 system clocking at over 12MHz. Proteus VSM also provides extensive debugging facilities including breakpoints, single stepping and variable display for both assembly code and high level language source.

System Components

ISIS Schematic Capture - a tool for entering designs.

PROSPICE Mixed mode SPICE simulation - industry standard SPICE3F5 simulator combined with a digital simulator.

ARES PCB Layout - PCB design system with automatic component placer, rip-up and retry auto-router and interactive design rule checking.

VSM - Virtual System Modelling lets cosimulate embedded software for popular micro-controllers alongside hardware design.

System Benefits Integrated package with common user interface and fully context sensitive help.

Download ISIS Proteus 7.1

(Due to an error, the link above was removed. Please check the link below for the update)


ISIS Proteus 7.6

      

Metronome

 
      

A metronome marks time by producing a regular sequence of "clicks" or "pocks". Adjust the click rate by adjusting R2 or changing C1's value. That will varying the RC time constant so it will also varying the "delay time" of the buzzer or speaker. This project is so simple, applicative and low-cost. It is suitable for you who loves to learn about music and build and use this project for your low-cost metronome. :-)



    

Light Flasher

 
         

This circuit produces bright flashes every second or so. R1 controls flash rate. L1 can replace with 3V or 4.5V flash light or for simply you can use a LED for example.

 

Zener Voltage Regulator

   
       

This circuit supplies a steady voltage (V_out) to a load from an unregulated supply (like a battery), V_in can vary but must be at least 1 volt above desired V_out. I, can vary from 0 mA to planned maximum value. I does not change if I_L falls to 0 mA. Since I = I_L + I_Z, I_Z rises as I_L falls. In other words, the regulator always uses the same current, even when the load is removed. Caution: D1 and R1 must have proper power rating. Use Ohm's Law.


Example:

A radio draws from 20 to 50 mA from a 9 volt battery. To power it from a 12 volt batery, use a 9 volt, 1/2 watt Zener Diode. R1 should be closed to 60 ohm and rated for at least 0.15 W.

     

Voltage Doublers

  
    

  

These circuit approximately double an incoming AC voltage. The output is DC. Use capacitors and diodes rated for twice the input voltage. Output ripple can be reduced by using large values for C1 and C2.


  

Fritzing (Electronics Software)

Fritzing is an open source GUI based program that allows users to document their prototypes, share them with others, show them in a presentation, and create a pcb layout for professional manufacturing. This is the latest version of Fritzing that released till today (version 0.5.2b). You can check for the Fritzing update directly on the Help tab on Fritzing window.

Download Fritzing 0.5.2b

Here's I give a quick tutorial using fritzing so it can help you to understand how to use fritzing more easily, have fun! :-)

Download Fritzing Quick Tutorial

Binary Subtraction

          Half subtractors and full subtractors will be explained in this section. The rules for the binary subtraction of two bits are given in Fig. 1. The top number in a subtraction problem is called the minuend. The bottom number is called the subtrahend, and the answer is called the difference. Rule 1 in Fig. 1 is obvious. Rule 2 (Fig. 1) concerns 1 being subtracted from the smaller number 0. In Fig. 2, note that, in the Is column of the binary number, 1 is subtracted from 0. A 1 must be borrowed from the binary 2s column, leaving a 0 in that column. Now the subtrahend 1 is subtracted from the minuend 10 (decimal 2). This leaves a difference of 1 in the Is column. The binary 2s column uses rule 1 (0-0) and is equal to 0. Therefore, rule 2 is 0 - 1 = 1 with a borrow of 1. Rules 3 and 4 are also rather obvious.

          The subtraction rules given in Fig. 1  look somewhat like a truth table. These rules have been reproduced in truth table form in Fig. 3. Consider the difference (Di) output in the truth table. Note that this output represents the XOR function. The logic function for the difference output in a subtractor is the same as that for the sum output in a half adder circuit. Now consider the borrow (Bo) column in the truth table. The logic function for this column can be represented by the Boolean expression A’ • B = Y. It can be implemented by using an inverter and a 2-input AND gate.

          The truth table in Fig. 3 represents a logic circuit called a half subtractor. The Boolean expression for the difference output is A(xor)B = Di. The Boolean expression for the borrow (Bo) output is A’ • B = Bo. A half subtractor would be wired from logic gates as shown in Fig. 4a. Input A is the minuend and B is the subtrahend. The Di output is the difference; Bo is the borrow. A simplified block diagram for a half subtractor is in Fig. 4b.

          Compare the half subtractor logic diagram in Fig. 4a with the half adder (in figure in the previous post). The only difference in the logic circuits is that the half subtractor has one added inverter at the A input of the AND gate.

          Consider the subtraction problem in Fig. 5. Several borrows are evident in this problem. If six subtractor circuits are used for the six binary places, the borrows must be considered. A half subtractor may be used for the Is place. Full subtractors must be used in the 2s. 4s. 8s. 16s. and 32s columns of this problem.

          A block diagram of a full subtractor (FS) is in Fig. 6. The inputs are A (minuend). B (subtrahend), and Bin (borrow input). The outputs are Di (difference) and Bo (borrow output). The Bo and Bin lines are connected from subtractor to subtractor to keep track of the borrows.

          The diagram in Fig. 6b shows how to wire two half subtractors (HS) and an OR gate together to form a full subtractor (FS) circuit. Note that the wiring pattern is similar to that used for adders. Finally, Fig. 7 shows how gates could be wired to form a full subtractor circuit. Remember that full subtractors must be used to subtract all columns except the Is column in binary subtraction. 

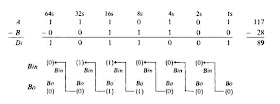
          The truth table for the full subtractor is in Fig. 8. The inputs are labeled as minuend (A), subtrahend (B), and borrow in (Bin). The outputs are the customary difference (Di) and borrow out (Bo).

          The binary subtraction problem in Fig. 9 will aid understanding of the full subtractor truth table. Follow as this problem is solved, using only the truth tables in Figs. 3 and 8. Look at the Is column of the problem in Fig. 9. The Is place uses a half subtractor. Find this situation in the truth table in Fig. 3. You find that line 3 of the half subtractor truth table gives an output of 1 for Di (difference) and 0 for borrow out (Bo). This is recorded below the Is column in Fig. 9.

          Consider the 2s column in Fig. 9. The 2s column uses a full subtractor. On the full subtractor truth table, look for the situation where A = 0, B = 0, and Bin = 0. This is line 1 in Fig. 8. According to the truth table, both outputs (Di and Bo) are 0. This is recorded below the 2s column in Fig. 9.

          Next consider the 4s column in Fig. 9. The inputs to this full subtractor will be A = 1, B = 1, and Bin = 0. Looking at the input side of the truth table in Fig. 8, it appears that line 7 shows this situation. The outputs (Di and Bo) are both 0 according to the truth table and are written as such on Fig. 9 under the 4s column.

          Look at the 8s column in Fig. 9. The inputs to the full subtractor will be A = 0, B = 1, and Bin = 0. Line 3 of the truth table (Fig. 8) shows this situation. The outputs (Di and Bo) in line 3 are both Is and are recorded in the 8s column in Fig. 9. 

          The 16s column in Fig. 9 has inputs of A = 1, B = 1, and Bin = 1. This corresponds with line 8 in the truth table. Line 8 generates an output of Di = 1 and Bo = 1. These Is are recorded under the 16s column in the problem.   

          The 32s column has inputs of A = 1, B = 0, and Bin = 1. This corresponds to line 6 in the truth table in Fig. 8. Line 6 generates outputs of Di = 0 and Bo = 0. These 0s are recorded in the 32s column of the problem. 

          Finally consider the 64s column in Fig. 9. The inputs to the full subtractor are A = 1, B = 0, and Bin = 0. This input combination is shown in line 5 in the truth table. Line 5 generates an output of Di = 1 and Bo = 0. Figure 9 illustrates how binary 11100 is subtracted from binary 1110101 using truth tables. The borrows are shown below the problem. This procedure is quite cumbersome for humans, but electronic circuits can accurately perform this subtraction in microseconds.

Binary Addition

          Adding binary numbers is a very simple task. The rules (addition tables) for binary addition using  two bits are shown in Fig. 8-1. The first three rules are obvious. Rule 4 says that, in binary, 1 + 1 = 10  (decimal 2). The 1 in the sum must be carried to the next column as in regular decimal addition.

Two sample binary addition problems are shown below:

          It is now possible to design a gating circuit that will perform addition. Looking at the left two columns of Fig.1 reminds one of a two-variable truth table. The binary rules are reproduced in truth table form in Fig. 3. The inputs to be added are given the letters A and B. The sum output is often given the summation symbol (∑). The carry-out output column is often just represented with the Co symbol.

          The truth table in Fig. 3 is that of a half adder circuit. A block diagram for a half adder might be drawn as in Fig. 4a. Note the two inputs A and B on the symbol in Fig. 4a. The outputs are labeled ∑ (sum) and Co (carry out). It is common to label the half adder with HA as shown on the block symbol.

          Looking at the sum (∑) output column of the truth table in Fig. 3, note that it takes an XOR function to produce the ∑ output. The carry-out column will use an AND function. A complete logic circuit for the half adder with two inputs (A and B) and two outputs (∑ and Co) is shown in Fig. 4b. Composed only of gates (XOR and AND), the half adder is classified as a combinational logic circuit.

          Consider the binary addition problem in Fig. 5a. The Is column is 1 + 1, and it follows rule 4 in Fig. 1. The sum is 0 with a carry of 1 to the 2s column. The 2s column must now be added. In the 2s column we have 1 + 1 + 1. This is a new situation. It equals binary 11 (decimal 3). The 1 is placed below the 2s column in the sum position. A 1 is carried to the 4s column. The single 1 at the top of the 4s column is added to the Os with a result of 1, which is written in the sum position. The result is a sum of 110.

          Rule 5 for binary addition is formally written in Fig. 4/5. Note the three inputs (A, B, and carry in). The outputs are the usual sum and carry out. Rule 5 suggests that a half adder will not work if a carry-in situation arises. Half adders will add only two inputs (A and B), as in the Is column of an addition problem. When the 2s column or the 4s column is added, a new circuit is needed. The new circuit is called a full adder. A block diagram of a full adder is shown in Fig. 6a.

          The full adder circuit has three inputs which are added. The inputs shown in the block diagram in Fig. 6 are A, B, and On (carry in). The outputs from the full adder are the customary ∑ (sum) and Co (carry out). Note the use of the letters FA to symbolize full adder in the block diagram. To repeat, the half adder is used in only the Is place when larger binary numbers are added. Full adders are used for adding all other columns (2s, 4s, 8s, and so forth).

          A full adder circuit can be constructed from half adders and an OR gate. A full adder circuit is diagrammed in Fig. 6b. The half adder becomes a basic building block in constructing other adders. A truth table for the full adder is detailed in Fig. 7.

Combinational Logic Circuit

          Multiple gate functions can be combined to form more complex or different Boolean logic functions. Wiring together multiple gates are used to build a complex logic function that only outputs a specific value when a specific combination of True and False inputs are passed to it is known as ‘‘combinatorial logic’’. The output of a combinatorial logic circuit is dependent on its input; if the input changes then the output will change as well.

          When I wrote the preceding paragraph, I originally noted that combinatorial logic circuits produce a ‘‘True’’ output for a given set of inputs. This is incorrect, as there will be some cases where you will require a False output in your application. I made the definition a bit more ambiguous so that you do not feel like the output has to be a single, specific value when the input consists of the required inputs. It is also important to note that in a combinatorial logic circuit, data flows in one direction and outputs in logic gates cannot be used as inputs to gates which output back to themselves. These two points may seem subtle now, but they are actually critically important to the definition of combinatorial logic circuits and using them in applications. 

          An example of a combinatorial circuit is shown in figure above. In this circuit, I have combined three AND gates, a NOR gate, a NOT gate and an XOR gate to produce the following logic function:

 This combinatorial circuit follows the convention that inputs to a gate (or a chip or other electronic component) are passed into the left and outputs exit from the right. This will help you ‘‘read’’ the circuit from left to right, something that should be familiar to you.

          While seeing a series of logic gates, like the one in figure above seems to be overwhelming, you already have the tools to be able to work through it and understand how it works. In the previous section, I noted that gates could be connected by passing the output of one into an input of another; a combinatorial circuit (like figure) is simply an extension of this concept and, being an extension, you can use the same tools you used to understand single gates to understand the multiple gate operation.

Logic Gates

          Various forms of logical building blocks are available in integrated circuit form. These logical building blocks are called “gates,” with each gate having a distinct function. Logic gates can be further combined into more complex digital building blocks to perform a variety of counting, memory, and timing functions. 

          Digital ICs are grouped into families, with each family possessing certain desirable traits that make them more or less suited to a variety of applications. One logic family might not be compatible with another family, so it is typical for the designer to use only one family type for each application. The most commonly used logic families in the present market are complementary metal oxide silicon (CMOS) and transistor-transistor logic (TTL). 

          Logic gates respond to “high” or “low” voltage levels. The specific voltage level for a “high” or “low” condition will vary from one logic family to another. For example, a logical one (high) in TTL logic is about 5 volts; in contrast, a possible 12-volt level might be used for CMOS logic. However, the functional operation and symbolic representation is universal throughout all of the families. In figure below lists some of the more common logic devices and their associated symbols. 

 

          Logic gates, and other logic devices, are functionally defined by using truth tables. The second figure illustrates a variety of truth tables for some common logic gates. Compare the AND-gate illustration in first figure with its corresponding truth table in second figure. Because the AND gate has two input leads, there are a total of four possible logic conditions that could occur on the inputs. Notice that the truth table lists the four possible input conditions; together with each of their resultant outputs for each condition. As shown by the truth table, the only time that the output goes “high” is when the A input “and” the B input are high. 

          Logic gates can have more than two inputs. Second figure illustrates the truth table for a three-input AND gate. Common logic gates are available with up to eight inputs. 

Referring again to first figure, note the OR gate and its associated truth table in second figure. As the name implies, its output goes high whenever a high appears on the A input, or on the B input (or both). 

In digital terminology, a not function means that a logical condition is inverted, or reversed. A NAND gate (short for not AND) is an AND gate, with the output inverted. Notice that the outputs in the truth tables for the AND gate, and the NAND gate, are simply inverted. This same principle holds true for the OR and NOR gates. 

          It is common for the output of one logic gate to provide inputs for several other logic gates. The maximum number of inputs that can be driven by a particular logic gate is specified as its fanout. Typical logic gates have fanouts ranging from 5 to 20. If it becomes necessary to drive a greater number of inputs than the fanout of a particular gate, a buffer is used to increase the fanout capability. The symbol for a buffer is illustrated in first figure. 

          The need often arises to invert a logic signal. The symbol for an inverter is shown in first figure. An inverter is sometimes called a not gate. Note that it has a small circle on its output just like the NOT AND (NAND) and NOT OR (NOR) gates. Anytime a small circle appears on an input or output of a logic device, it is symbolizing the inversion of the logic signals (or data). Also notice the horizontal line above the A output of the inverter. It is called a not symbol. Whenever a horizontal line is placed above a logic expression, it means that it is inverted. 

          Another common type of logic gate is the exclusive OR gate. Refer to its symbol and the associated truth table in first and second figures. As the truth table indicates, its output only goes high when its inputs are different from each other. The exclusive NOR gate provides the same logic function with an inverted output.

Introduction to Digital Electronics

Digital electronics is a large branch of the electrical-electronics field relating to those electronic functions used in performing logical functions. It encompasses every type of logical system from simple combinational logic control in a coffee pot to the largest computer systems. The concept of digital control is not new. Even before the first computer appeared, or solid-state electronics came into being, large banks of relays were performing logical control functions in industrial facilities.

          The earliest types of computers were called analog computers. They were enormous machines made from thousands of vacuum tubes. Computations were performed using voltage levels based on the decimal (base 10) numbering system. Although this method seems natural because you think in terms of tens (because you were created with 10 fingers), the old analog computers soon gave way to the more modern binary computers (base 2). There are very good reasons for this change, which will be explained as this chapter continues. 

          Although many people seem to have trouble comprehending different numbering systems, it’s really quite simple. The key is in understanding the mechanics behind the decimal system, and then applying those principles to any other numbering system. 

          The term decimal means “base 10.” If the number 1543 is broken down into decimal column weights, it comes out to 3 units (or ones), 4 tens, 5 hundreds, and 1 thousand. Notice how each succeeding weight is actually the base number (10) times the “weight” of the preceding column. In other words, 1 x 10 = 10, 10 x 10 = 100, 10 x 100 = 1000, and so on. 

          The binary numbering system works exactly the same way, except that it is based on 2 instead of 10. For example, the first weight (or least significant digit) is the units, or ones, column. The weight of the second column is 2 x 1, or 2. The next column is 2 x 2, or 4. The next column is 2 x 4, or 8. Instead of the column weights being ones, tens, hundreds, thousands, ten thousands, and so forth, the binary column weights will be ones, twos, fours, eights, sixteens, and so on. 

          In the decimal system, there are 10 possible numbers which can be placed in any weight column (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). In the binary system, there are only two possible numbers for any one weight column (a 0 or a 1; a “yes” or a “no”; an ON or an OFF). If a binary number such as 0111 is broken down into weights, it means 1 one, 1 two, 1 four, and 0 eights. By adding the weights together, the binary number can be converted to decimal. In the previous example, 1 + 2 + 4 = 7. Therefore, 0111 is the binary equivalent to decimal 7. 

          The following example demonstrates how it is possible to count up to 9 using the binary numbering system:

The binary numbering system is used in digital electronics because the binary digits 1 and 0 can be represented by an electronic device being either ON or OFF. For example, a relay can be energized or deenergized; or a transistor can be saturated or cut off. The advantage to a simple ON/OFF status is that the “absolute value or voltage level is not important.” In other words, it is totally irrelevant whether a transistor in cutoff has 4.5 volts, or 5.5 volts, on its collector. The only important data from a binary point of view is that it is OFF. 

          There are other numbering systems used extensively in digital electronics besides the binary system. The two most common ones are the octal system (base 8) and the hexadecimal system (base 16 system). These different numbering systems come in handy when interfacing with humans, but at the actual component level, everything is performed in binary.

Analog VS Digital

          However, there are instances in which the input signal is naturally discrete in form, e.g., pulses from a particle detector, or "bits" of data from a switch, keyboard, or computer. In such cases the use of digital electronics (circuits that deal with data made of 1's and 0's) is natural and convenient. Furthermore, it is often desirable to convert continuous (analog) data to digital form, and vice versa (using D/A and A/D converters), in order to perform calculations on the data with a calculator or computer or to store large quantities of data as numbers. In a typical situation a microprocessor or computer might monitor signals from an experiment or industrial process, control the experimental parameters on the basis of the data obtained, and store for future use the results collected or computed while the experimcnt is running.

          Another interesting example of the power of digital techniques is the transmission of analog signals without degradation by noise: An audio or video signal, for instance, picks up "noise" while being transmitted by cable or radio that cannot be removed. If, instead, the signal is converted to a series of numbers representing its amplitude at successive instants of time, and these numbers are transmitted as digital signals, the analog signal reconstruction at the receiving end (done with D/A converters) will be without error, providing the noise level on the transmission channel isn't high enough to prevent accurate recognition of 1's and 0's. This technique, known as PCM (pulse-code modulation), is particularly attractive where a signal must pass through a series of "repeaters," as in the case of a transcontinental telephone call, since digital regeneration at each stage guarantees noiseless transmission. The information and pictures sent back by recent deep space probes were done with PCM. Digital audio is now commonplace in the home, in the form of 12cm optical "compact discs" (CDs); these store a piece of music in the form of a stereo pair of 16-bit numbers every 23 microseconds, 6 billion bits of information in all.

          In fact, digital hardware has become so powerful that tasks that seem well suited to analog techniques are often better solved with digital methods. As an example, an analog temperature meter might incorporate a microprocessor and memory in order to improve accuracy by compensating the instrument's departure from perfect linearity. Because of the wide availability of microprocessors, such applications are becoming commonplace. Rather than attempt to enumerate what can be done with digital electronics, let's just start learning about it. Applications will emerge naturally as we go along.